避免四舍五入输入

数值问题的一个常见来源是用于表示约束矩阵系数的数字的数值四舍五入。为了说明这个问题，考虑下面的例子:

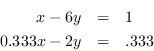
$\begin{eqnarray*} x - 6y &=&1\\ 0.33x - 2y &=& .333 \end{eqnarray*}$

人们可能很容易认为这两个方程是等价的，但将两者都加入一个模型将导致一个不正确的结果。这对我们的用户来说是很重要的一点:Gurobi始终相信他们提供的输入数字，并且永远不会更改它们，除非这些更改能够证明不会影响解决方案。

因此，考虑到这一点，在前溶解期间，Gurobi可以使用第二个约束来确定:

$\begin{displaymath} y:= 0.1665x - 0.1665 \end{displaymath}$

当代入第一个约束条件时，它会产生

$\begin{eqnarray*} x - 6\cdot(0.1665x - 0.1665) &=& 1\\ \Leftrightarrow 0.001 &=& 0.001 \end{eqnarray*}$

因此

作为唯一的解决方案。

如果用户提供了这两个方程:

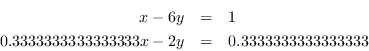
$\begin{eqnarray*} x - 6y&=&1\\ 0.3333333333333333333333 x - 2y&=&0.333333333333 \$

这将给:

$\begin{displaymath} y:= 0.166666666667x - 0.1666666666666667 \end{displaymath}$

收益率:

$\begin{eqnarray*} x - 6\cdot(0.16666666666667x - 0.166666666666666666666667x) &=& 1\\ \Leftrightarrow 2\cdot10^{-16} x + 1 + 2\cdot10^{-16} &约& 1\结束{eqnarray*}$

即使有一个很小的阈值来处理系数为零，这里的结果是第一个约束确实是多余的。任何解决方案

被认为是可行的

的主要观点是,约束是完全平行,或线性相关(双精度浮点和小公差内)是无害的,但几乎是相互平行的约束产生微小系数线性系统解决了预处理,可以肆虐的解决方案的过程。在下一节中，我们将对极限进行扩展双精度浮点数字，尤其是为什么 $< span > < / span > 1美元\大约1 + 2 \ cdot10 ^ {-16} < span > < / span >美元$ ．