处理epsilon - 最佳解决方案

处理epsilon - 最佳解决方案

上一节认为是多个（真实）最佳解决方案的情况。当我们有几个时会发生什么- 优化的解决方案？更具体地说，考虑

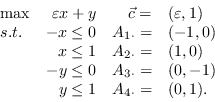
图形方式可以描绘为如果是零，然后我们处于以前描述的情况。但是，注意，客观载体的小扰动可能导致或者被报告为最佳。和宽容可以在这里发挥重要作用。如果例如，是否定的，然后将是数学上的最佳结果，但由于最优耐受性，Simplex可能会得出结论是最佳的。更准确地说，如果小于默认的最优性容差然后，Simplex可以自由地声明最佳解释（在公差范围内）。

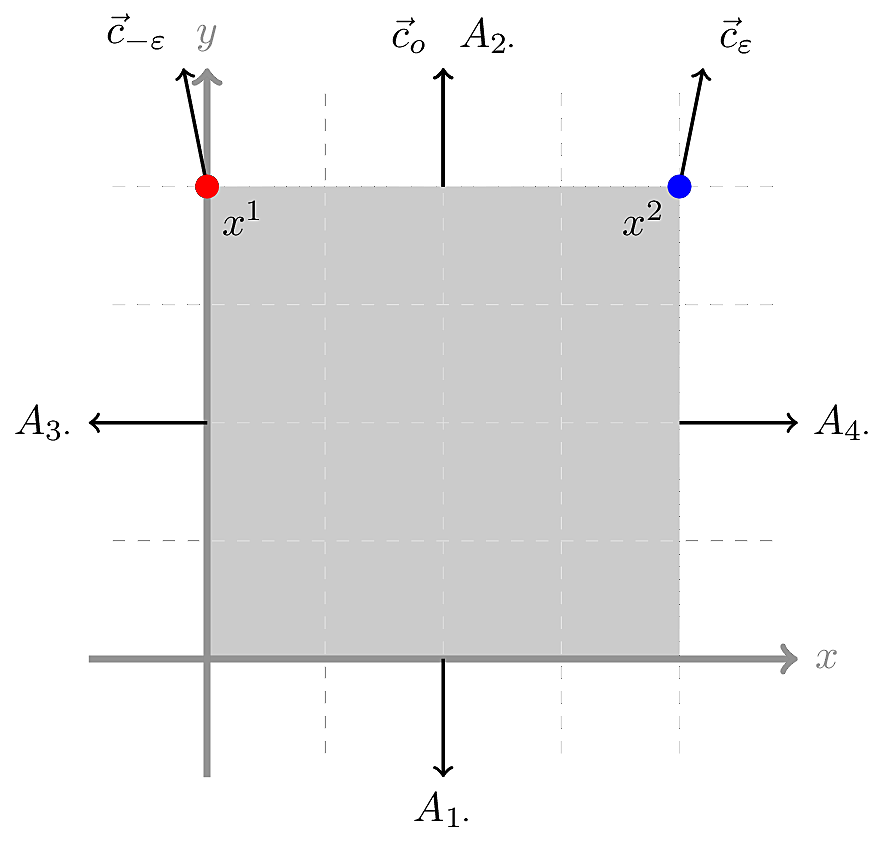
以上陈述是如此距离之间和不是太大了。要看到这一点，请考虑当我们改变右侧时会发生什么从1到。然后，可行区域将是一个非常长的矩形盒，顶点那那和。也许有点令人惊讶，如果低于双重容差，单纯x可以考虑最佳，即使它的客观价值是，这可以在最终目标价值方面非常相关。

请注意，两种情况共享一个成分：目标函数（几乎）平行于可行区域的一个侧面。在第一种情况下，这一侧相对较短，因此跳跃到转化为客观价值的小变化。在第二种情况下，几乎平行于目标函数的一侧很长，现在跳跃到可以对最终目标函数产生重大影响。

如果您取出这两种成分中的任何一种，即客观的矢量几乎平行于约束，或者边缘由这个近似平行的约束引起的很长，那么这个问题无法出现。出于本节开始时讨论的原因，客观函数很常见于平行于一个或多个约束。因此，避免这种情况的最佳方法是避免第二条件。最简单的方法是确保变量的范围不太大。请参考缩放关于此指导的部分。