线性优化问题的几何形状

在显示出现不良行为的优化模型之前，我们首先需要了解几何学在他们后面。考虑表单的问题

$\ begin {displaymath} \ begin {array} {ll} \ max＆cx \\ s.t.＆ax \ leq b。\\ \ end {array} \结束{displaymath}$

例如：

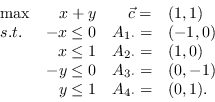
$\ begin {displaymath} \ begin {array} {lrrl} \ max＆x + y＆\ vec {c} =＆（1,1）\\ s.t.＆-... ...点} =＆（0，-1）\\＆y \ leq 1＆a_ {4 \ cdot} =＆（0,1）。\\ \ end {array} \ END {displaymath}$

请注意，如果我们表示

，那么问题可以说明

$\ begin {displaymath} \ max_ {x \ in \ mathbb {r} ^ 2} \ {\ vec {c} x：ax \ leq b \}。\结束{displaymath}$

可行的区域，改善方向 $ $ \ vec {c} $ $ 和最佳解决方案

可以描绘为

请注意，每当我们朝着方向移动时 $ $ \ vec {c} $ $ ，价值 $ $ \ vec {c} x $ $ 增加。此外，由于我们无法移动

对于具有更好的客观价值的另一个可行点，我们可以得出结论

确实是问题的最佳解决方案。注意

是A.角落可行区域的点。这不是巧合;如果有界区域，您将始终在角点找到最佳解决方案 $ $ \ vec {c} $ $ 不是零。如果目标为零，那么所有可行的解决方案都是最佳的;我们将更多地讨论零目标及其含义后来。

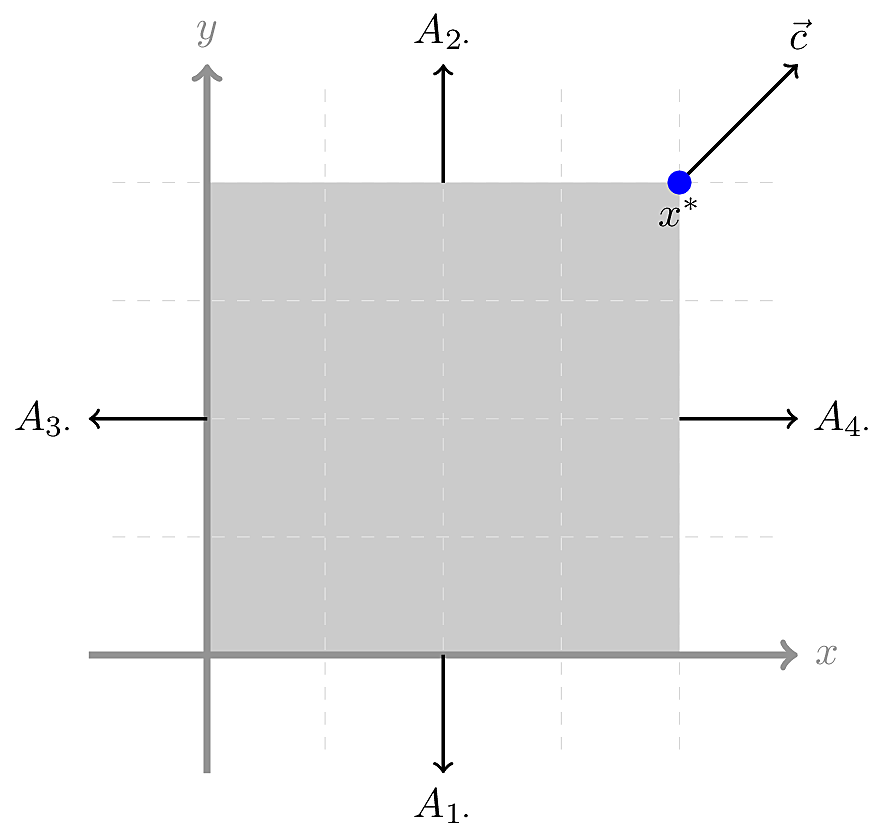
要了解输入数据的变化如何影响可行区域和最佳解决方案，请考虑一个小修改： $ $ \ tilde {b} ^ t =（\ varepsilon，1,0,1） $ $ 那 $ $ \ tilde {\ vec {c}} =（1+ \ varepsilon，1） $ $ ，和 $ $ \ tilde {a_ {4 \ cdot}} =（\ varepsilon，1） $ $ 。然后我们的优化问题看起来像

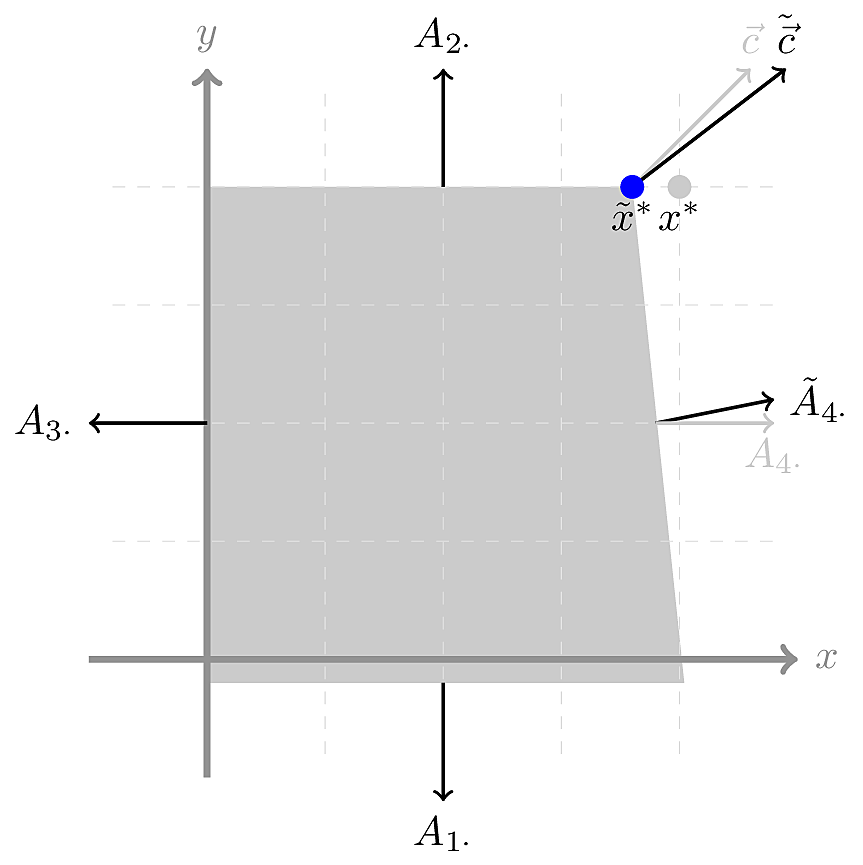
请注意，虽然我们改变了右侧，但这种变化对问题的最佳解决方案没有影响，但它通过扩大可行区域的底部来改变可行区域。

改变目标矢量在图形表示中倾斜相应的向量。这当然还会改变最佳目标值。扰动约束倾向于约束的图形表示。变化 $ $ a_ {4 \ cdot} $ $ 改变原始解决方案本身。大量的倾斜约束经历取决于扰动的相对值。例如，虽然约束 $ $ x \ leq 1 $ $ 和约束 $ $ 100 x \ LEQ 100 $ $ 诱导相同的可行区域，扰动 $ $ x + \ varepsilon y \ leq 1 $ $ 会诱导更多的触摸扰动 $ $ 100 x + varepsilon y \ leq 100 $ $ 。